La costante di Boltzmann: ponte tra mondo microscopico e macroscopico
La costante di Boltzmann rappresenta uno dei pilastri fondamentali della fisica moderna, ma spesso rimane un concetto astratto per chi non ha dimestichezza con la materia. In realtà, questa costante governa fenomeni che sperimentiamo quotidianamente: dalla pressione dell'aria che respiriamo al funzionamento del termostato di casa, dal comportamento dei gas nelle nostre cucine fino ai principi che regolano il riscaldamento domestico. Comprendere la costante di Boltzmann significa scoprire il legame invisibile tra il movimento frenetico degli atomi e molecole che ci circondano e i fenomeni macroscopici che osserviamo ogni giorno nella nostra abitazione.
Cos'è la costante di Boltzmann e come si ricava
Non bisogna andare molto lontano per trovare tale costante, dal momento che è nascosta, per così dire, nella legge dei gas perfetti. L'equazione di stato dei gas perfetti, nella sua versione più nota è utilizzata è:
P V = n R T
Dove:
- P è la pressione del gas
- V è il volume
- n è il numero di moli
- R è la costante universale dei gas (8,314 J/(mol·K))
- T è la temperatura assoluta (espressa in Kelvin)
Per comprendere meglio questa relazione, pensiamo a situazioni concrete della vita quotidiana. Quando gonfiamo un pneumatico della bicicletta, stiamo aumentando la pressione P inserendo più molecole d'aria (aumentando n) in un volume V fisso. Quando una bombola del gas si scalda al sole, la temperatura T aumenta e di conseguenza aumenta anche la pressione interna.
Se adesso portiamo il volume al secondo membro dell'equazione, avremo:
P = nm R T
dove nm è la densità molare data dal rapporto n/V. A sua volta, la densità molare nm può essere riscritta come: ρ/Na, dove ρ è la densità numerica (una grandezza che esprime il rapporto fra numero di molecole del gas e il volume) e Na è il numero di Avogadro, una costante fondamentale pari a 6,022 × 10²³ mol⁻¹.
Ebbene, possiamo riscrivere la legge dei gas perfetti come:
P = ( ρ R T ) / Na
La costante di Boltzmann, indicata con Kb (o più comunemente kB), è definita proprio come il rapporto fra costante universale dei gas R e numero di Avogadro Na:
Kb = R / Na
Si tratta quindi di una costante che è il rapporto tra altre due costanti fondamentali. Il valore numerico della costante di Boltzmann è 1,380649 × 10⁻²³ J/K, dove J rappresenta i joule (unità di energia) e K i kelvin (unità di temperatura).
La forma più potente della legge dei gas e i suoi significati fisici
Pertanto, la legge di stato dei gas perfetti si può scrivere in una forma meno comune di quella di partenza ma decisamente più potente:
P = ρ Kb T
In questa forma possiamo vedere come la pressione esercitata da un gas dipende esclusivamente dalla sua temperatura, essendo gli altri termini delle costanti. Maggiore sarà la temperatura del gas, maggiore sarà la pressione esercitata dallo stesso.
Questo fenomeno ha spiegazioni pratiche molto concrete. Quando accendiamo i fornelli della cucina, il gas che brucia si riscalda e tende ad espandersi, creando correnti convettive che distribuiscono il calore. Allo stesso modo, quando l'impianto di riscaldamento domestico si attiva, l'aria calda diventa meno densa e sale verso l'alto, mentre l'aria fredda scende, creando la circolazione naturale che riscalda gli ambienti.
Questo perché all'aumentare della temperatura aumenta lo stato di agitazione termica delle molecole di gas, vale a dire la loro energia cinetica media, e aumenterà il numero di urti di tali molecole contro le pareti del recipiente.
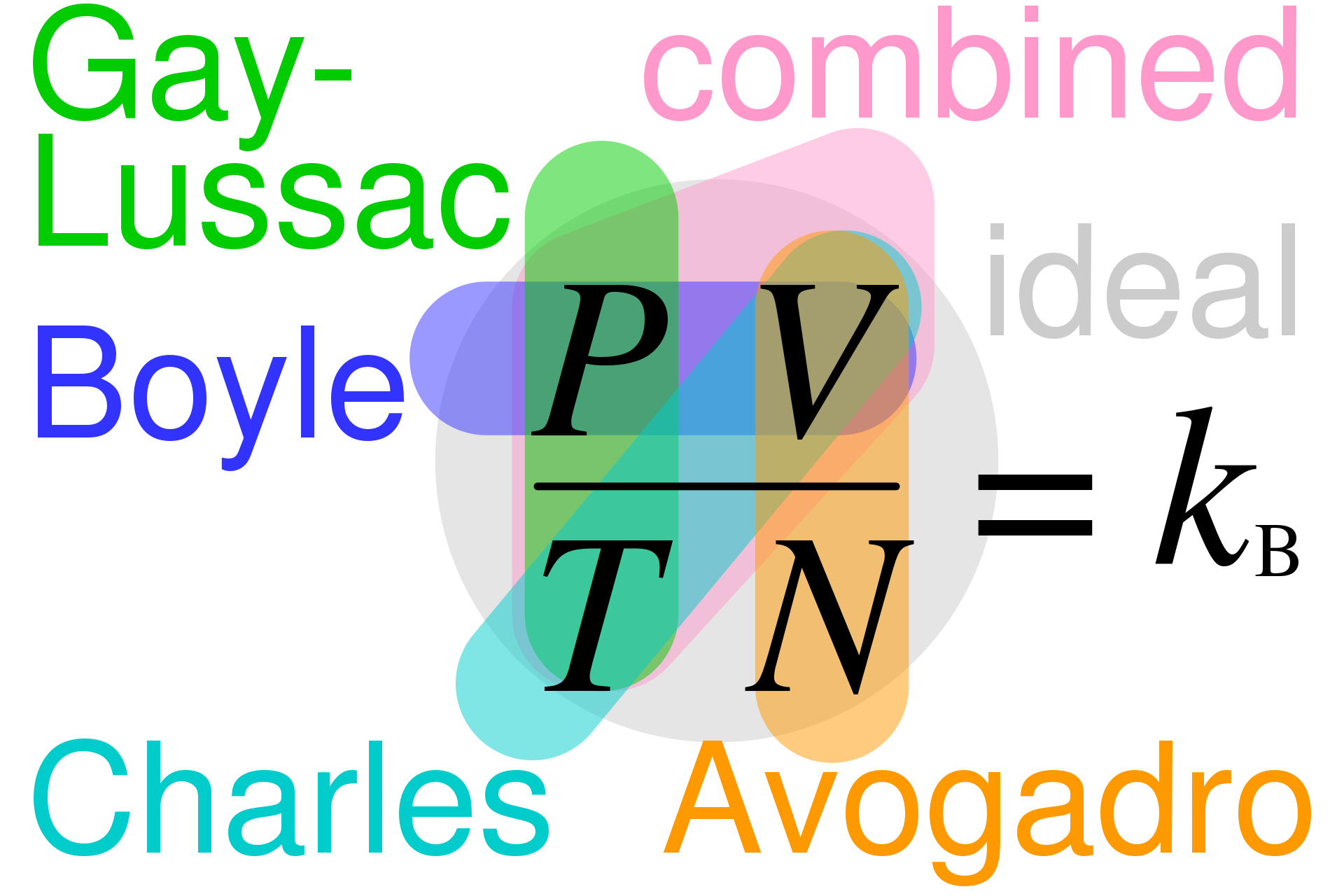
A livello macroscopico vediamo un incremento di temperatura, a livello microscopico c'è un aumento dell'energia cinetica media delle particelle. A fare da ponte fra questi due mondi macro e micro c'è la costante di Boltzmann.
Siccome la densità di numero ρ può essere anche espressa come rapporto fra numero di molecole N e volume V, allora possiamo riscrivere anche nella seguente forma:
P = (N Kb T) / V
riportando il volume al primo membro si ha:
PV = NKbT
Poiché il prodotto PV è costante, ne consegue che anch'esso dipende solo dalla temperatura, nell'ipotesi che il numero N di molecole di gas rimanga costante nel tempo. Sotto questa ipotesi, un gas composto da N molecole, vede la sua pressione aumentare all'aumentare della temperatura, e viceversa.
Applicazioni pratiche e fenomeni quotidiani
P e V sono fra loro inversamente proporzionali: diminuendo il volume si ottiene una compressione del gas e un incremento della sua temperatura, a causa degli urti fra particelle. Questo principio è alla base di molte applicazioni quotidiane.
Per esempio, quando premiamo il pistone di una pompa per bicicletta, stiamo riducendo il volume dell'aria al suo interno. Secondo la relazione PV = costante (a temperatura fissa), la pressione aumenta proporzionalmente. Se pompiano rapidamente, possiamo anche notare che il corpo della pompa si scalda leggermente: questo è dovuto all'energia che si trasforma in calore durante la compressione.
Un altro esempio pratico riguarda le pentole a pressione. In questi dispositivi, il vapore acqueo non può espandersi liberamente a causa del coperchio sigillato. Secondo l'equazione PV = NkBT, se il volume V è limitato e la temperatura T aumenta (a causa del riscaldamento), la pressione P deve necessariamente aumentare. Questo permette all'acqua di bollire a temperature superiori ai 100°C, riducendo i tempi di cottura.
Curiosità fisica: La costante di Boltzmann ha le stesse unità di misura dell'entropia e della capacità termica (J/K). Questo non è un caso: l'entropia, che misura il disordine di un sistema, è intimamente legata al movimento caotico delle particelle a livello microscopico, movimento che la costante di Boltzmann aiuta a quantificare.
Quindi fra mondo microscopico e mondo macroscopico c'è la costante di Boltzmann a fare da raccordo. Nello specifico la costante di Boltzmann è pari a 1,38 × 10⁻²³ J/K e ha le stesse unità di misura dell'entropia e della capacità termica.
Ludwig Boltzmann fu il primo a mettere in relazione entropia e probabilità nel 1877, gettando le basi della meccanica statistica. La sua celebre equazione S = k ln W (dove S è l'entropia, k è la costante di Boltzmann e W è il numero di microstati possibili) è incisa sulla sua tomba a Vienna, testimonianza dell'importanza di questa scoperta.
Il video illustra i concetti fondamentali della costante di Boltzmann e le sue applicazioni nella fisica moderna.
Domande frequenti sulla costante di Boltzmann
Qual è la differenza tra la costante di Boltzmann e la costante universale dei gas?
La costante di Boltzmann (kB = 1,38 × 10⁻²³ J/K) si riferisce a singole particelle, mentre la costante universale dei gas (R = 8,314 J/(mol·K)) si riferisce alle moli. Sono legate dalla relazione R = kB × NA, dove NA è il numero di Avogadro.
Perché la costante di Boltzmann è così importante in fisica?
Rappresenta il ponte tra il mondo microscopico (singole molecole) e quello macroscopico (gas e temperatura osservabili). Permette di collegare l'energia cinetica media delle particelle con la temperatura che misuriamo, fondamentale per la termodinamica e la meccanica statistica.
Come si manifesta la costante di Boltzmann nella vita quotidiana?
Ogni volta che osserviamo fenomeni legati alla temperatura e alla pressione: dalla cottura in pentola a pressione, al riscaldamento domestico, dalla condensazione sui vetri fino al funzionamento di termometri e barometri. È alla base di tutti i processi termici.
La costante di Boltzmann cambia con la temperatura o la pressione?
No, è una costante fisica fondamentale, invariabile. Il suo valore è fissato per definizione dal Sistema Internazionale dal 2019. Ciò che cambia sono le variabili (temperatura, pressione, volume) nell'equazione che la contiene.
Qual è il legame tra costante di Boltzmann ed entropia?
L'entropia di Boltzmann è definita come S = kB ln W, dove W rappresenta il numero di microstati possibili del sistema. Questa relazione mostra come il disordine macroscopico (entropia) sia legato alle configurazioni microscopiche delle particelle attraverso la costante di Boltzmann.
La costante di Boltzmann rappresenta quindi uno degli strumenti più eleganti della fisica per comprendere come il mondo infinitamente piccolo delle molecole si rifletta nei fenomeni che sperimentiamo quotidianamente. Come disse Albert Einstein: "Attraverso la costante di Boltzmann, possiamo misurare la quantità di disordine presente in un sistema e comprendere i principi dell'entropia".
Si ringrazia il Dott. Luigi Rescigno per il supporto scientifico.